Cryptography Time Capsule

I was looking at Robert Smithson’s Yucatan mirrors. I started thinking about buried or hidden art, and how it might be rediscovered by future art archeologists.

• 

• 

It brings to mind pyramids lost to time and much later discovered, also in the Yucatan.

It is easy enough to hide something. But more difficult for it to stay hidden, especially over time. And given our relentless development of every square inch of everything, difficult indeed.

And would whatever you hid be worth the trouble of finding in the future? That’s an open question of course. If you are Robert Smithson or the unnamed Yucatan builders, perhaps. But for the rest of us?

So assuming that you chose a good hiding place and that that future generations were interested in finding your surprise, how would you keep the location secret? How do you prepare an information time capsule?  I started thinking about encryption.

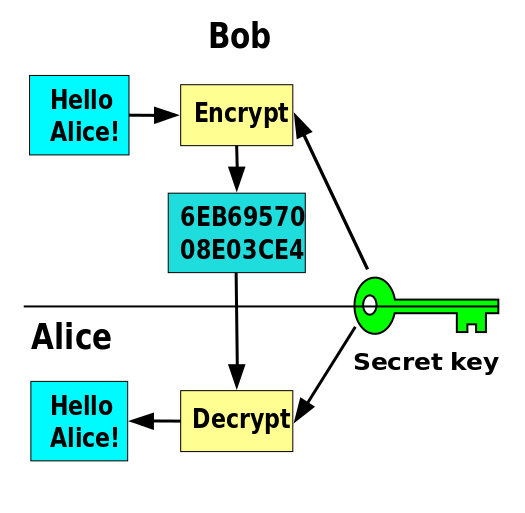
Bear with me while I explain the very basics of cryptography. We’re going to try to frame modern encryption as a way to securely wrap up a message to the future.

Your computer uses encryption to keep your information safe and private. That means it turns data such as your credit number into unreadably garbled text such as 243c33914a7bbe0d0ff7f9765d9b9 before sending it over the internet. The original plain text and a secret key are run through some encryption algorithm. The effectiveness of the encryption depends on the strength of the algorithm and the length of the key used.

While different methods of encryption may have weaknesses that make them easier to crack, at worst case an attacker may just attempt to guess the key. The process of methodically running through all the possible keys is called a brute-force keyspace search.

An example: If you knew what algorithm I used and I told you that I encrypted a sentence with a single Latin letter key, you’d immediately see that it would take you at most 26 tries to crack my code. (You’d know you’d guessed correctly when intelligible words emerged at the end of the process.) If I told you I’d used two Latin letters, at the worst case it would take you 26 x 26, or 676 tries. As the key size increases, so do the possible number of combinations. 676 tries might take you a while by hand, but it would take a computer no time at all.

An aside: Keys are not the same as passwords. To prevent it from being guessed, keys need to be truly random and contain enough disorder in their bit patterns. When a password or passphrase is used as an encryption key, randomness (in the form of a random number called a “salt”) is added and it is stretched or compressed to the right length.

Fun fact: When choosing a password, length is the only thing that influences password strength (so says a 2011 Carnegie-Mellon study that has since been confirmed). So all your fancy 133t substitutions and funky punctuation characters don’t really matter, because your 8 character password can be cracked in under a day.

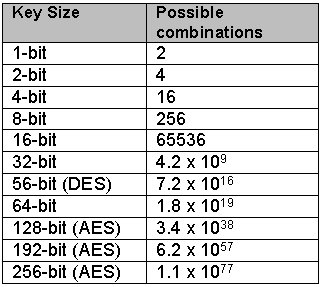
Key strength is generally measured not in numbers of characters, but in the number of bits that compose those characters. When you hear about encryption, you’ll frequently hear schemes that use 128-, 256-, and 512-bit encryption.

For a given key-length, the number of possible combinations is a power of two, or 2^n where n is the key length. A 128-bit key has 2 to 128th power combinations. That’s 3.4 x 10^38 (or 340 billion billion billion billion billion billion billion billion billion billion billion billion) combinations. That’s a lot. It might take a while to get through all these possibilities. These numbers get surprisingly large surprisingly fast. Burt Kaliski (as quoted by Cory Doctorow) came up with this analogy:

Imagine a computer that is the size of a grain of sand that can test keys against some encrypted data. Also imagine that it can test a key in the amount of time it takes light to cross it. Then consider a cluster of these computers, so many that if you covered the earth with them, they would cover the whole planet to the height of 1 meter. The cluster of computers would crack a 128-bit key on average in 1,000 years.

So to methodically guess a very long key takes a long long long time.

That said, two things are on the side of the cracker: 1) every year increases in computing power make it faster to crack encryption keys, and 2) over time, weaknesses are found in algorithms and their implementations decreasing bit strength. Given time, you can expect any encryption to be cracked. But in general, given a good algorithm (and the hope that it won’t be completely cracked later), one choses key strength corresponding to how long one wishes a secret to remain hidden.

Or put another way, every encryption is a time capsule for the future. Now we’re talking about the riddle that hides our art gift to the future.

Your web browser uses “asymmetric encryption” (meaning the the key used to encrypt a message is not the same as the key used to decrypt it) that is roughly half as effective as symmetric encryption. Most web technologies use 128-bit asymmetric encryption which is relatively easy for a dedicated cryptanalyst to crack. More security-conscious applications use 256-bit encryption.

A few specific algorithms have been cracked at 512-bits. Products touting the security of their encryption typically use 1024- or 2048-bit encryption. 4092-bit encryption exists and is in the “tin-foil hat” category of encryption. At these high-levels of encryption, it is virtually certain that the encryption algorithm will be cracked long before the key is.

So if you wanted to leave a gift for the future, one could easily enough craft a message including the GPS coordinates of your future art gift and encrypt it with a decent algorithm and a high-order key. Then one would put the encrypted message out into the world and wait a few hundred years for people to discover where you’d put it.

And hopefully, when they know where to look, it is still there.

And hopefully, someone still cares.